Leveraged returns in Marginly pools

Leveraged returns
It's a commonly known fact in finance that leverage amplifies market returns. To prove that this fact works for Marginly, let’s build from the basic example of a single user position to the portfolio of 2 positions which we can generalize to any arbitrary number of positions.
Single user long position
Let's assume the following:
- User brings margin M in base token
- User buys M * (L - 1) base tokens to get leverage L
- Buy price is P₀
- Market price of the base token in terms of quote token at time t is Pₜ
Then the user's net position at time t₁ is:
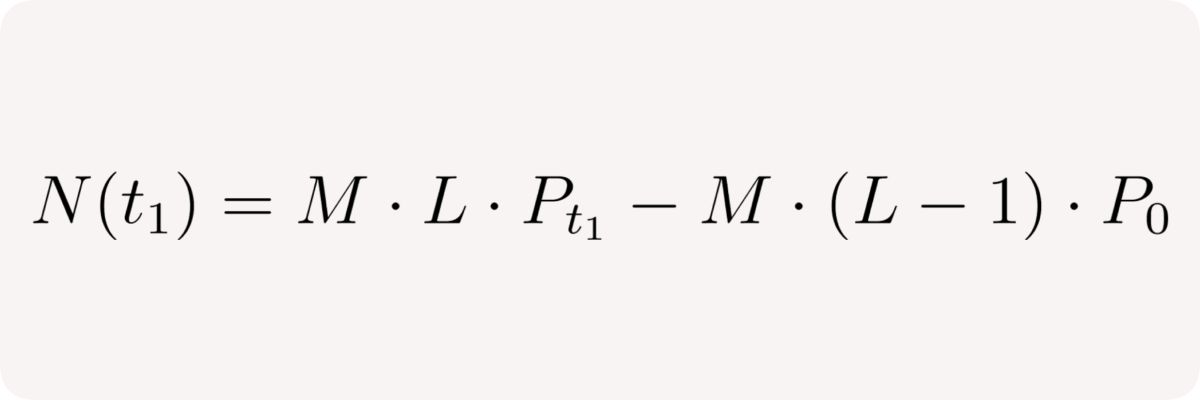
Then the change of the user's net position between times t₁ and t₂ is:
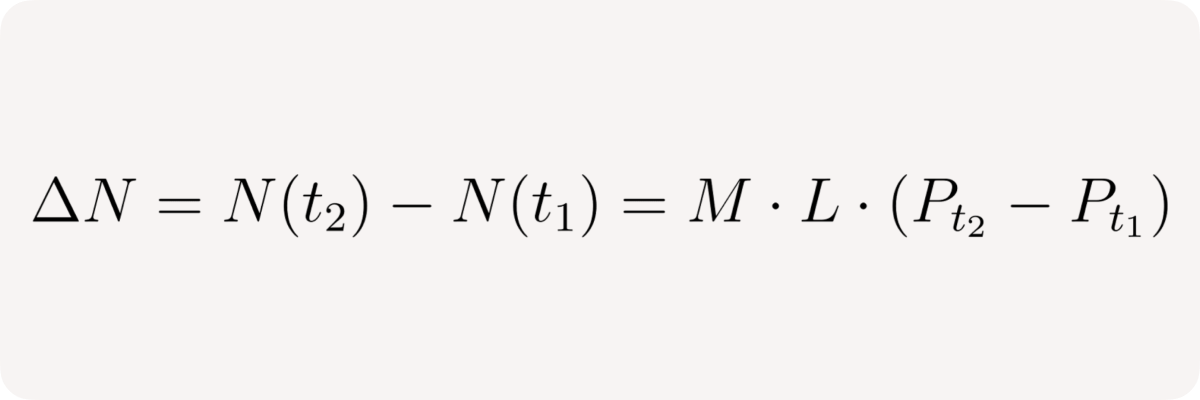
or in relative terms:
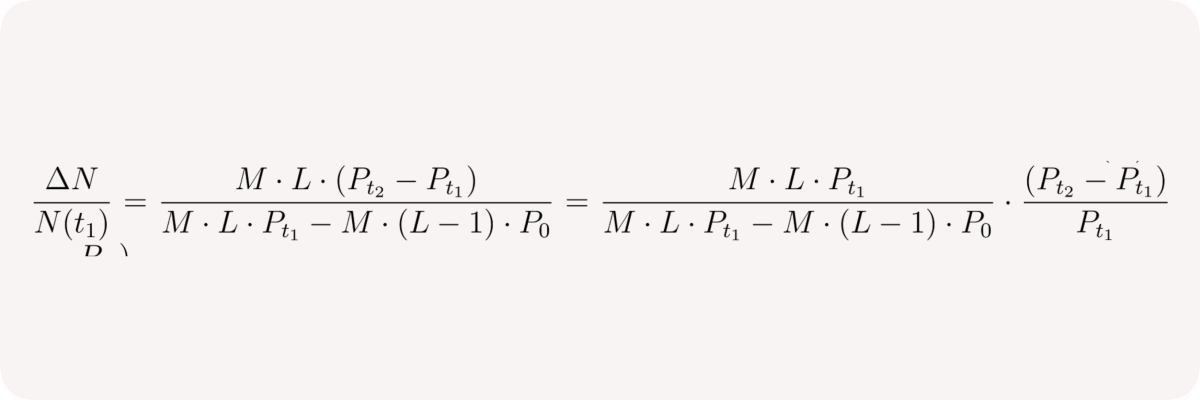
The left fraction is the current position leverage at time t₁:
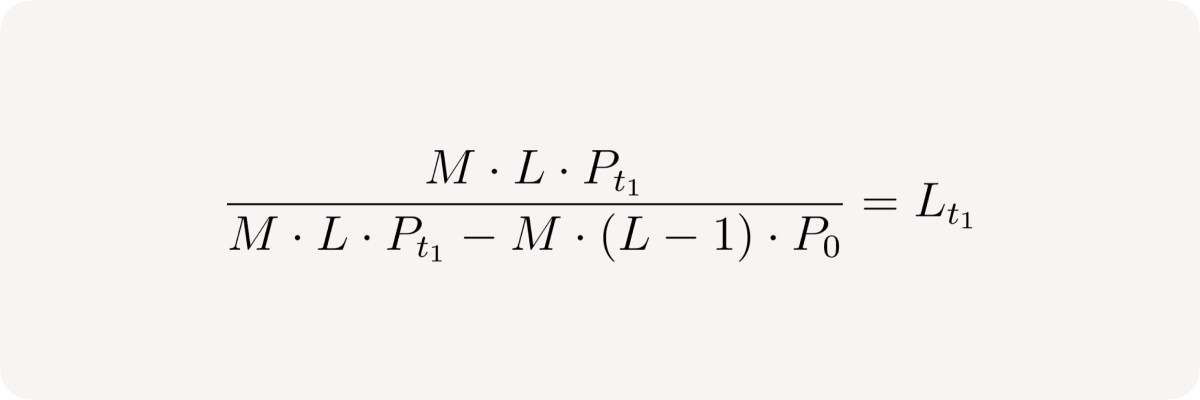
The right fraction is the market return between t₂ and t₁:
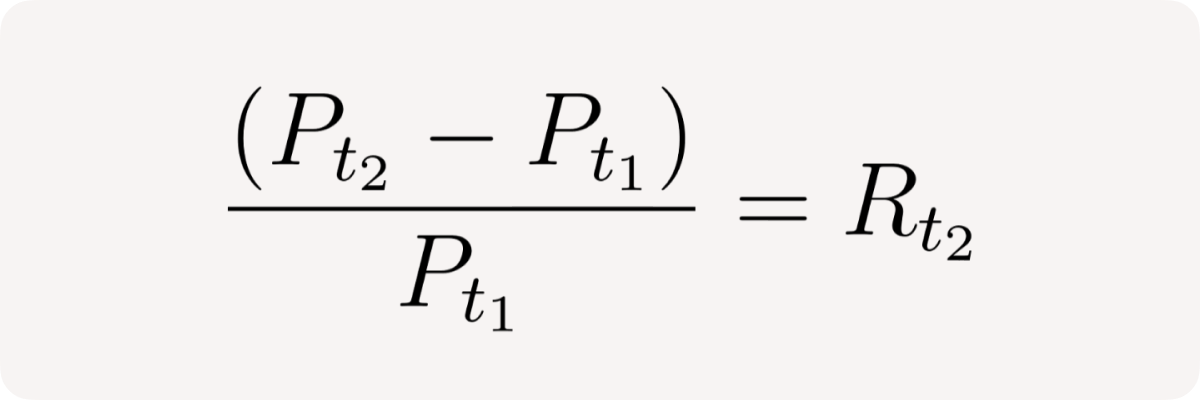
so, finally, the relative net position change between times t₁ and t₂ is:
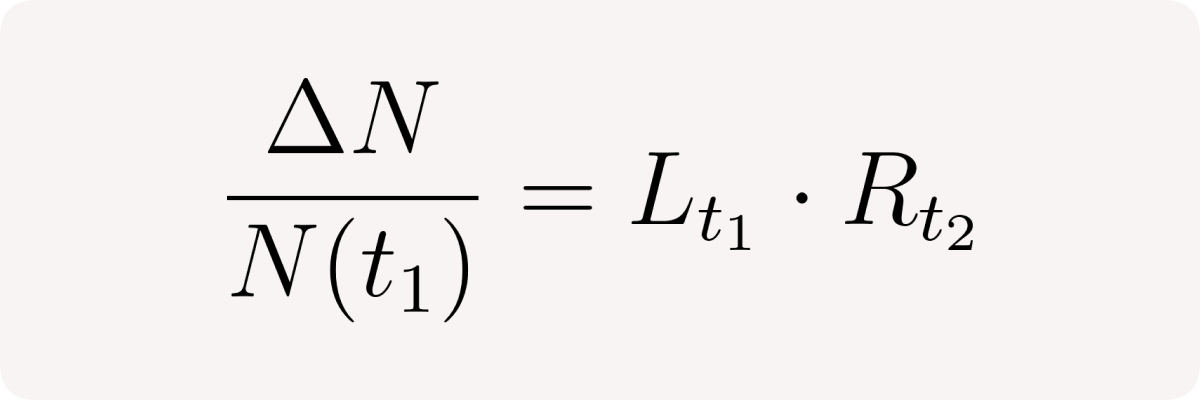
The user getting leverage automatically gets his market return amplified (levered) by the amount of the leverage.
Single user short position
- User brings margin M in quote token
- User receives M * (L - 1) quote tokens to get leverage L
- Sell price is P₀
- User effectively sells M * (L - 1) /P₀ base tokens
- Market price of the base token in terms of quote token at time t is Pₜ
User's net position at time t₁:
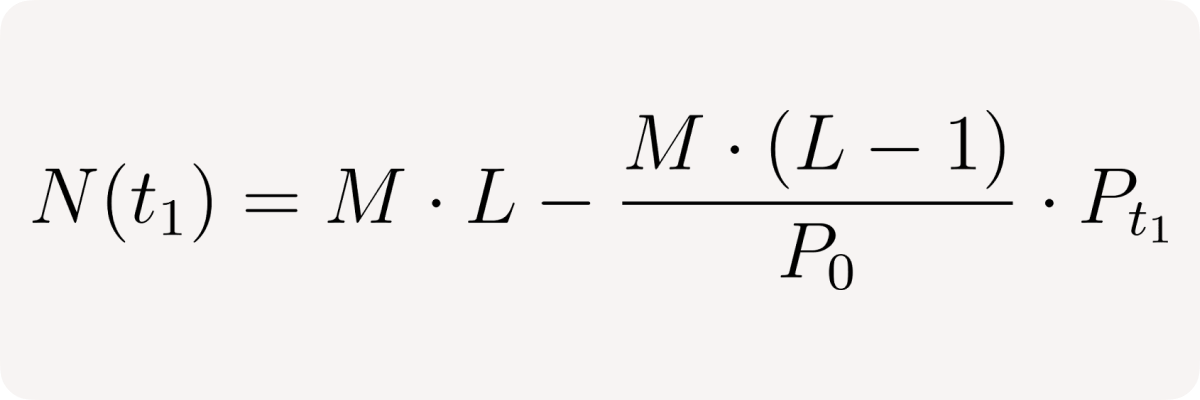
The change of the user's net position between times t₁ and t₂ is:
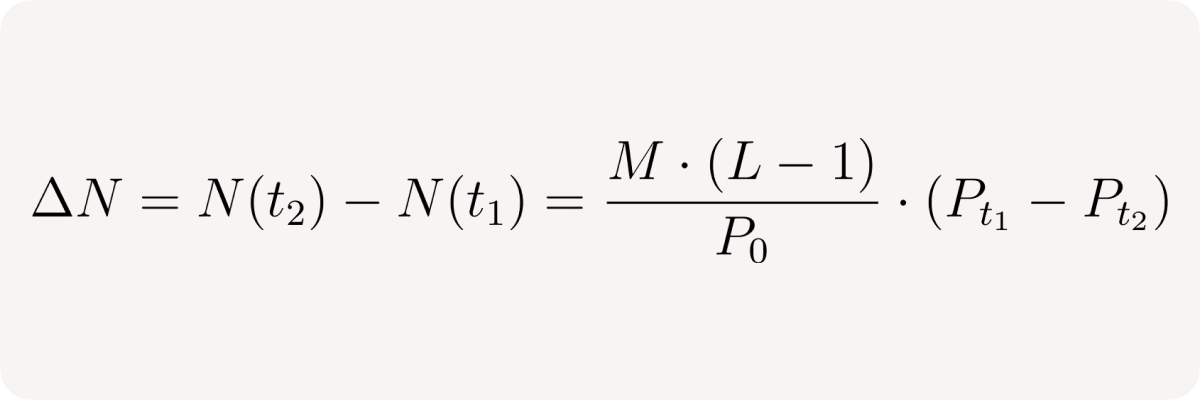
or in relative terms, similarly to the long case above:
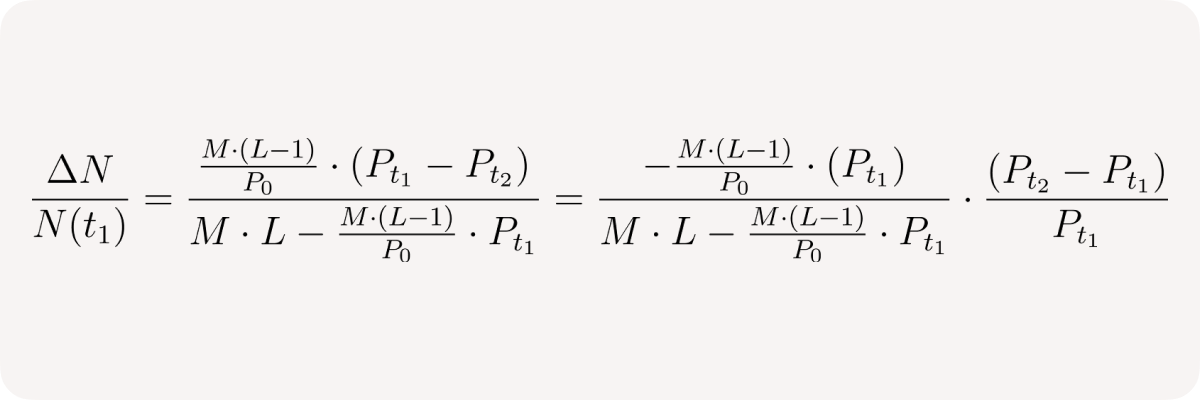
the first fraction is
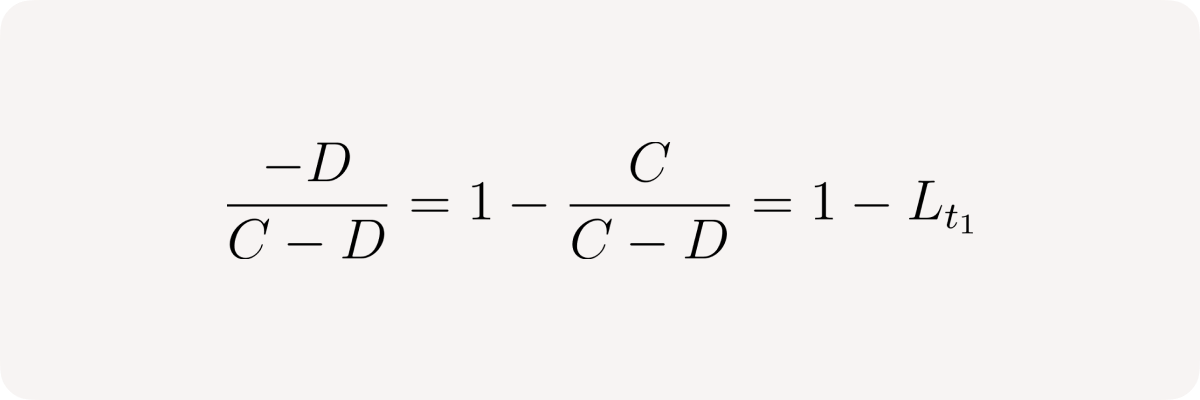
while the second one is market return Rₜ₂ again, so we end up with:
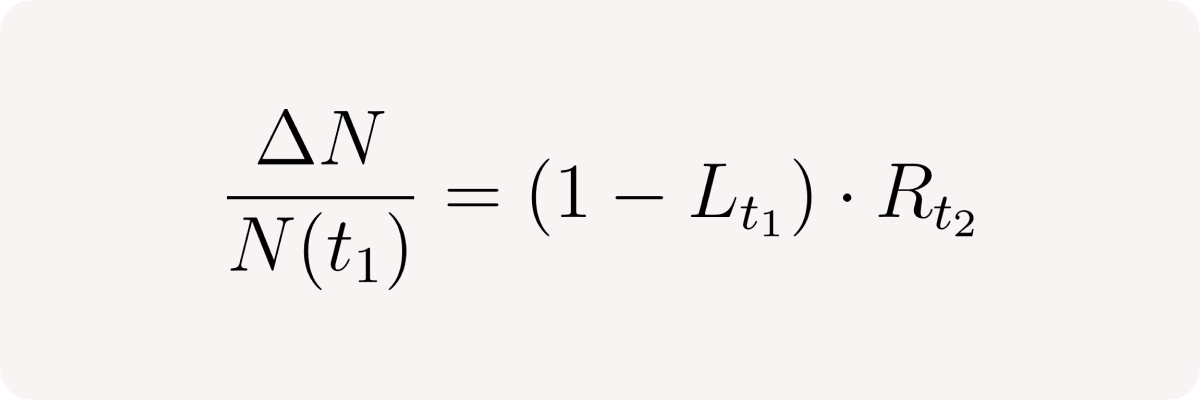
Pool long position
Consider 2 users to derive relationship for the pool
User net positions:
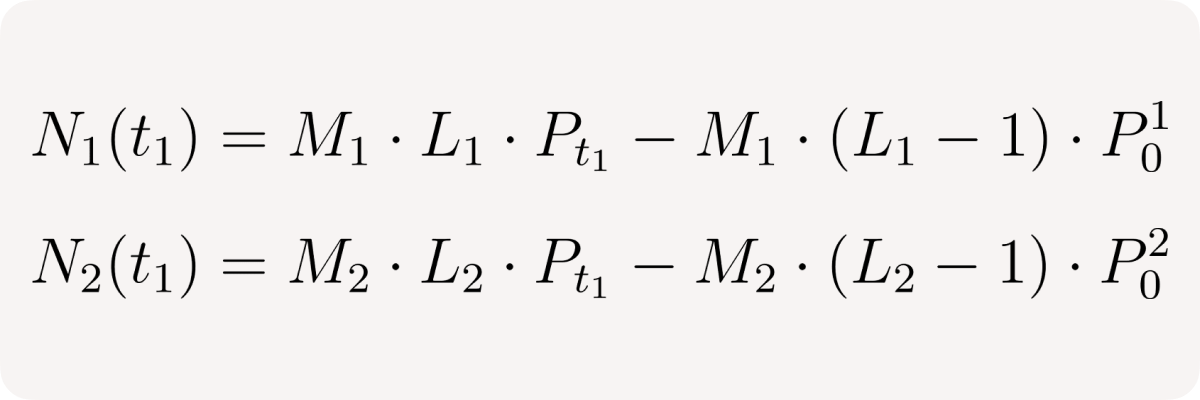
Pool net position:
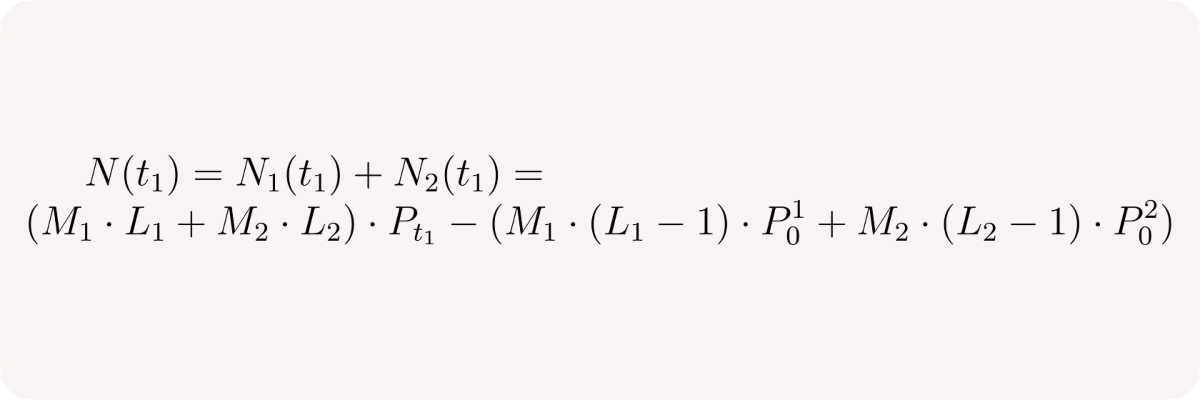
Let's denote:
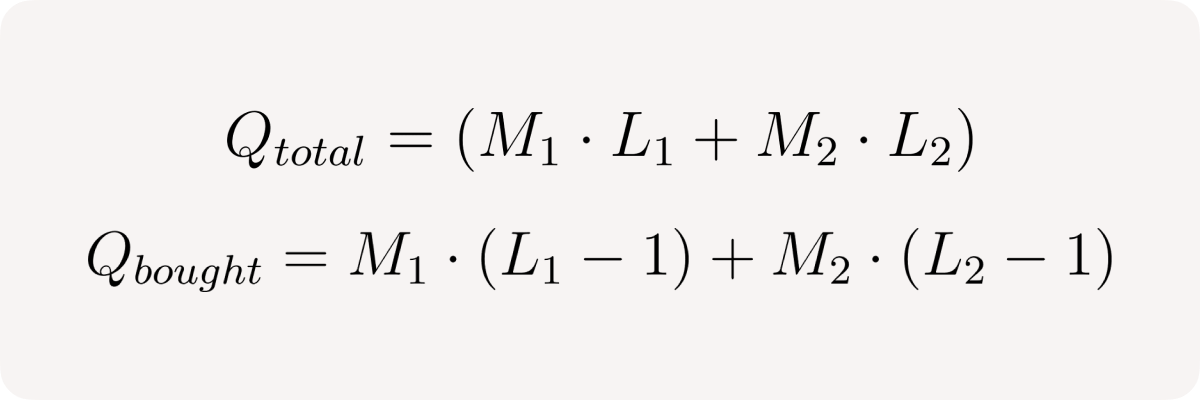
Then we can rewrite pool's net position in terms of Qtotal and Qbought:
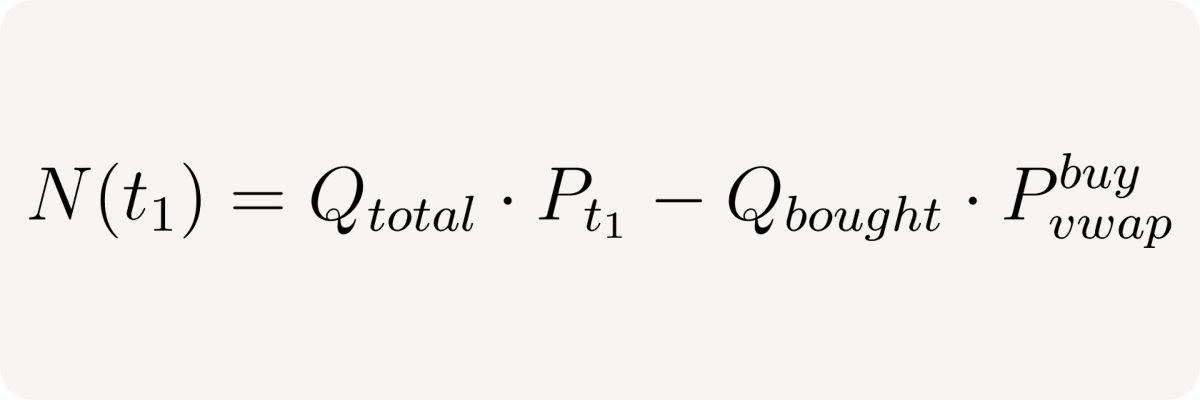
Now let's consider change in pool's net position or delta between times t₁ and t₂ given that no other trades occur in between:
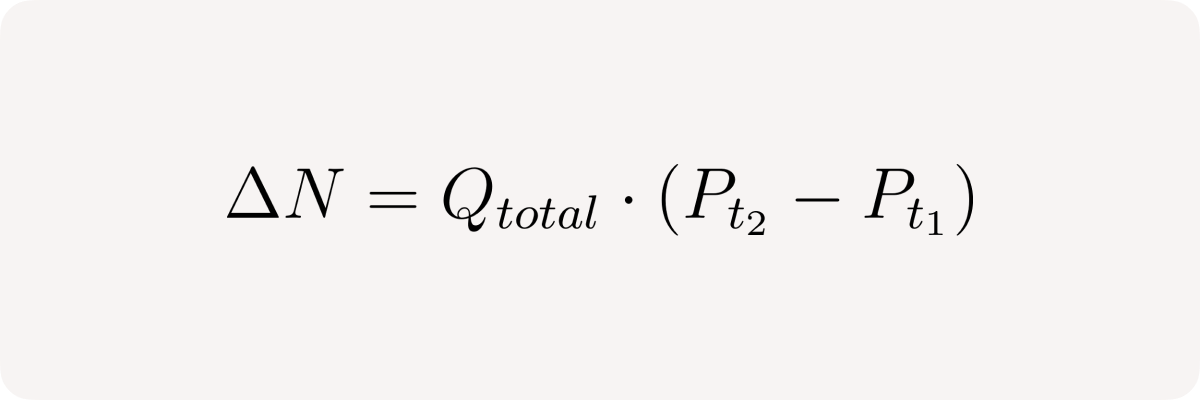
and finally in relative terms:
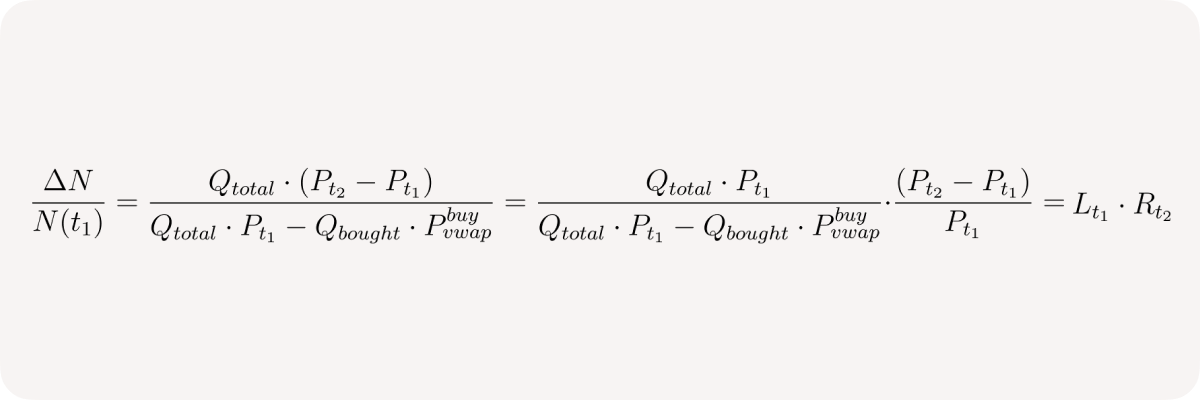
We observe the same result as for a single user, which is expected, given we can treat our pool as a single user making multiple long trades.
Pool short position
User's net position at time t₁:
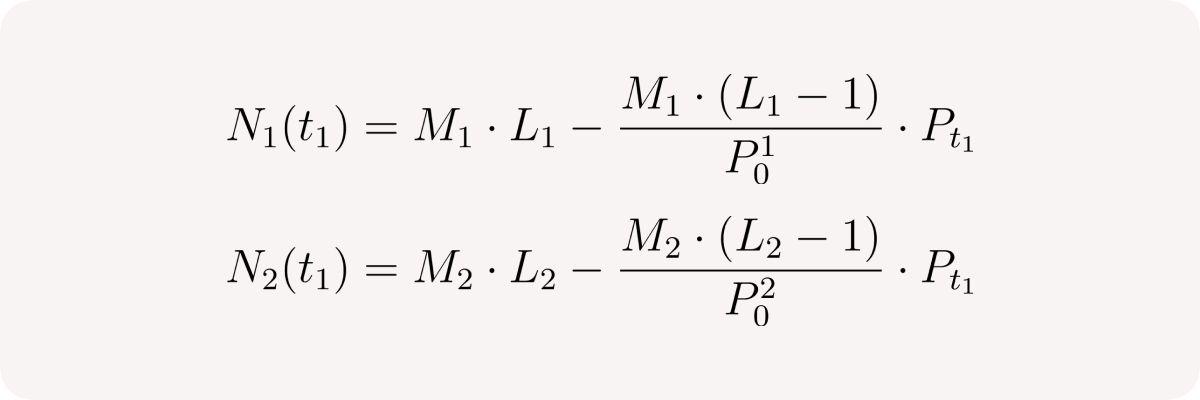
Pool net position:
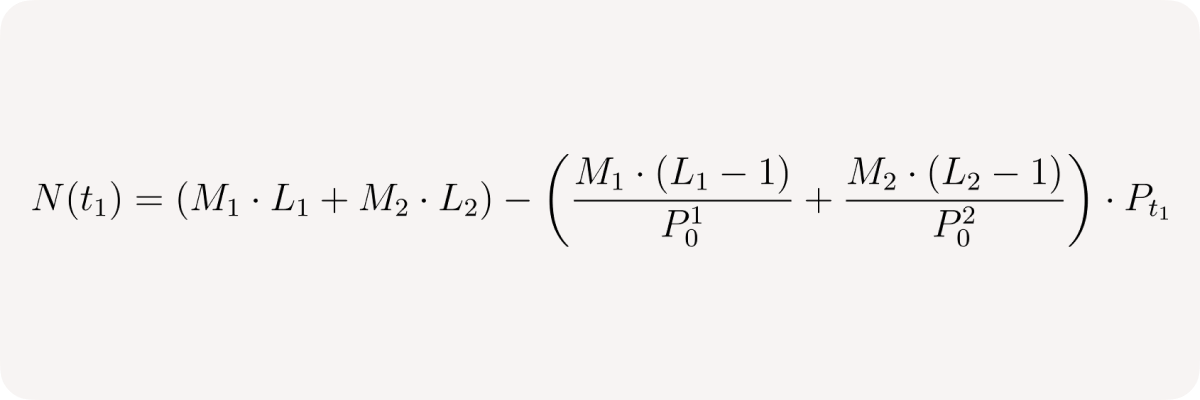
Pool net position:
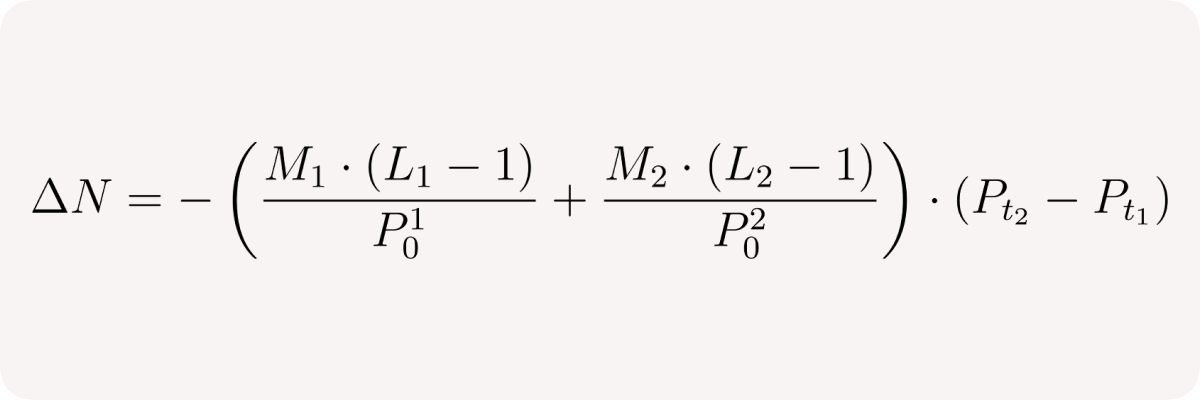
Similarly we can denote the total amount of base tokens sold:
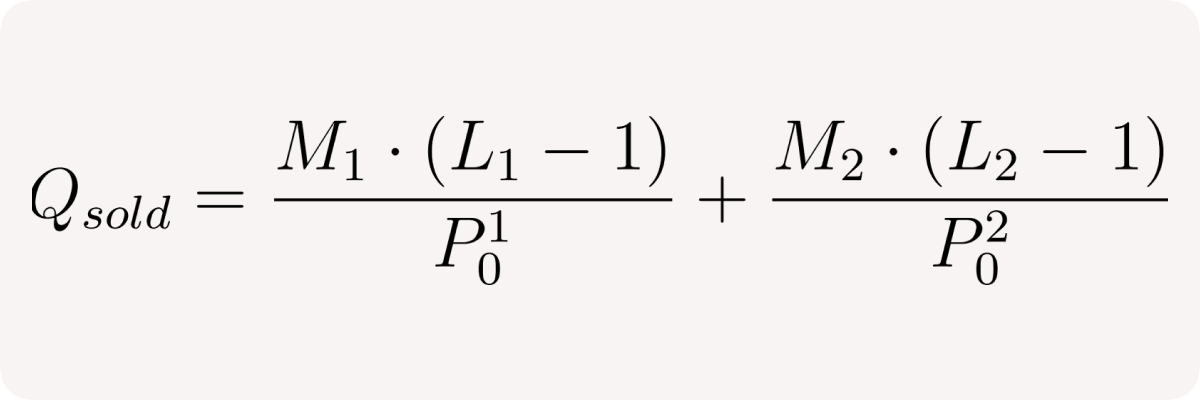
then the total quote token collateral is
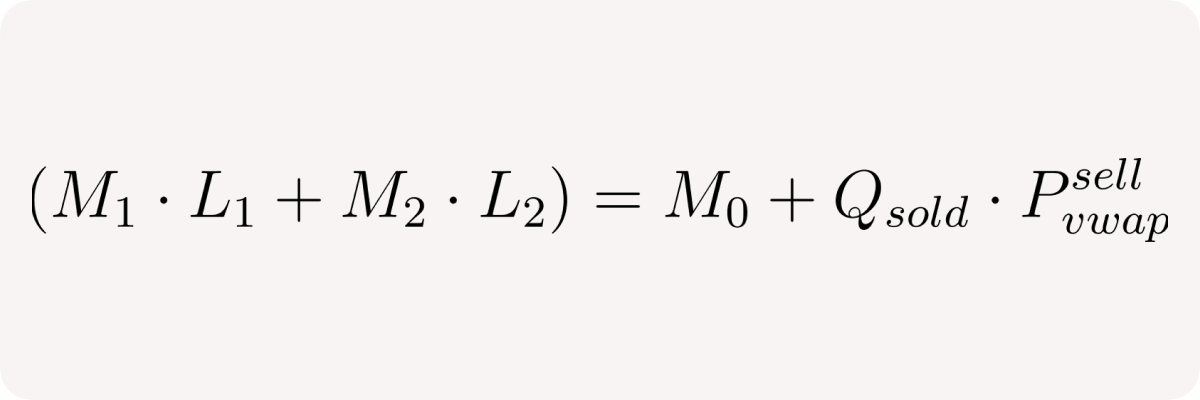
where M₀ is initial quote token margin, then the pool short leverage is
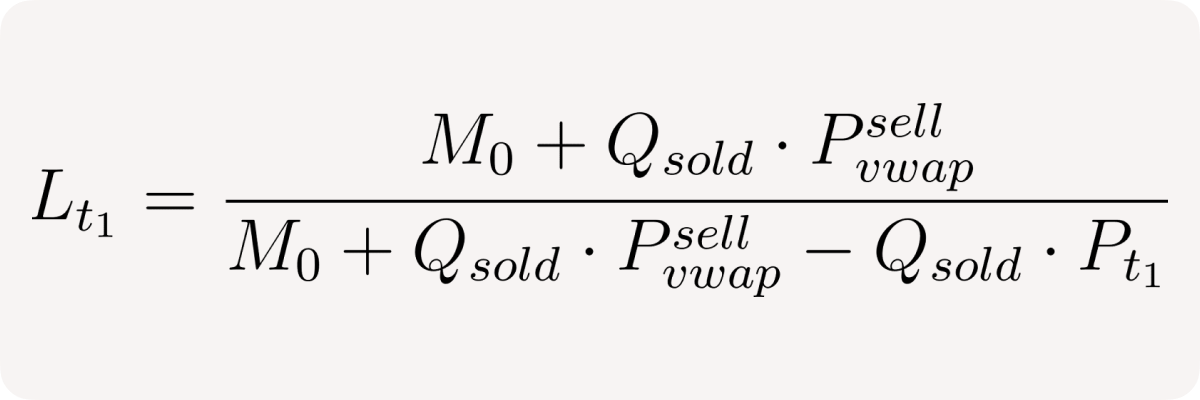
and finally, the pool's relative net position change is the same as for a single short user.
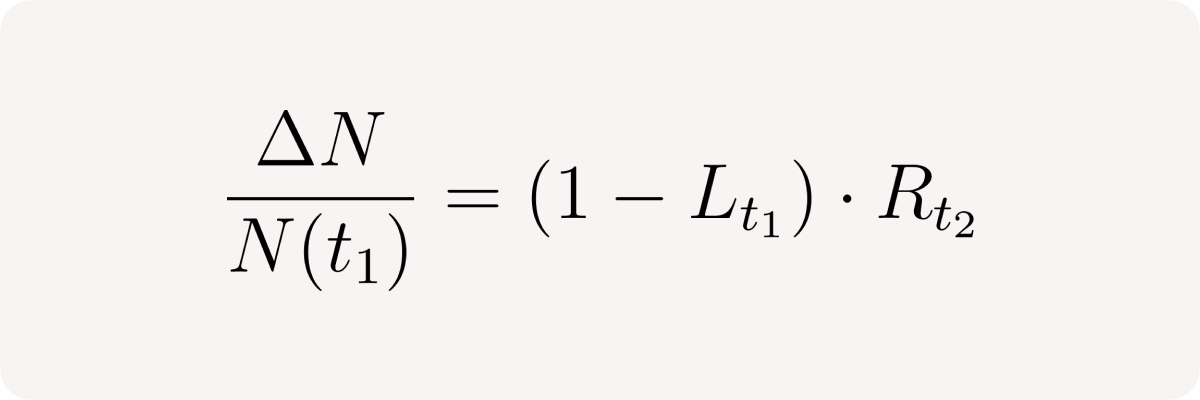
Pool net position
Now let's combine long and short pool net positions and the combined Net position as well:
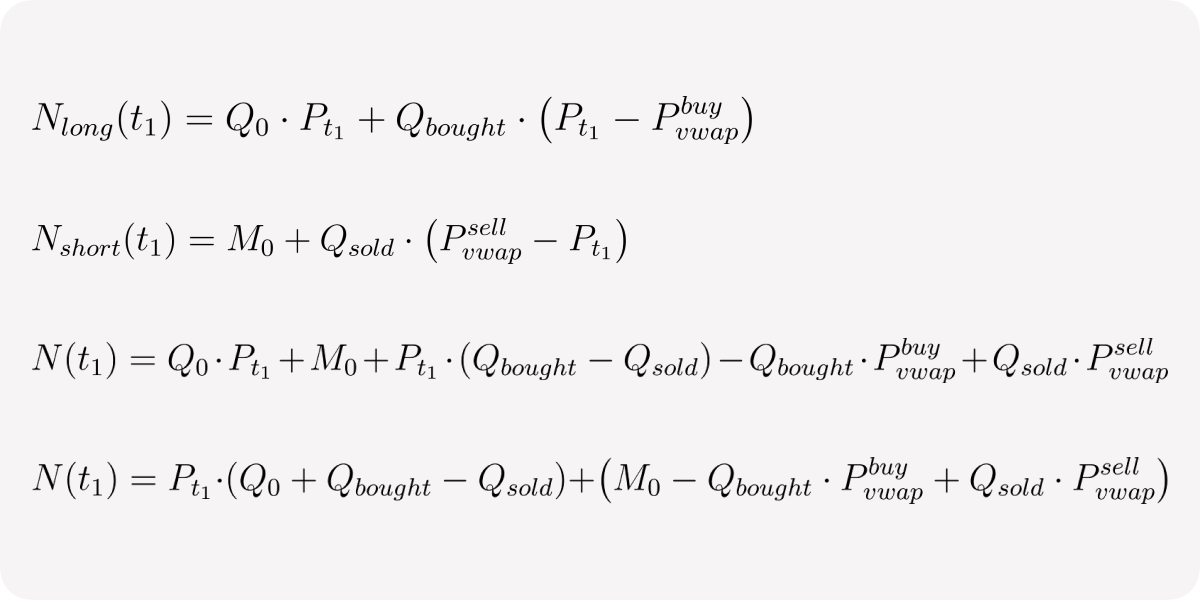
First two formulas show that both long Net position and short Net position consist of initial margin (first term) and the PnL (second term). Slightly reorganizing the terms for the total net position we can observe that net position tracks current balances value of both quote and base assets. Written in this form it shows us that the balanced system is when Qbought = Qsold and Pvwap buy = Pvwap sell
Leveraged returns and implications
The formulas for relative position changes may be used to define return and/or price bands until the respective net position is effectively 0 (decreases by 100%)
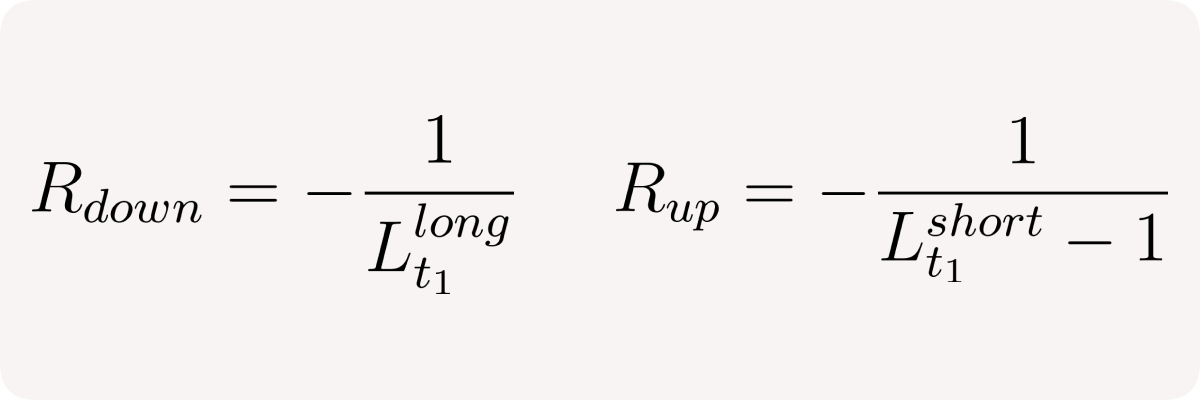
or for prices:
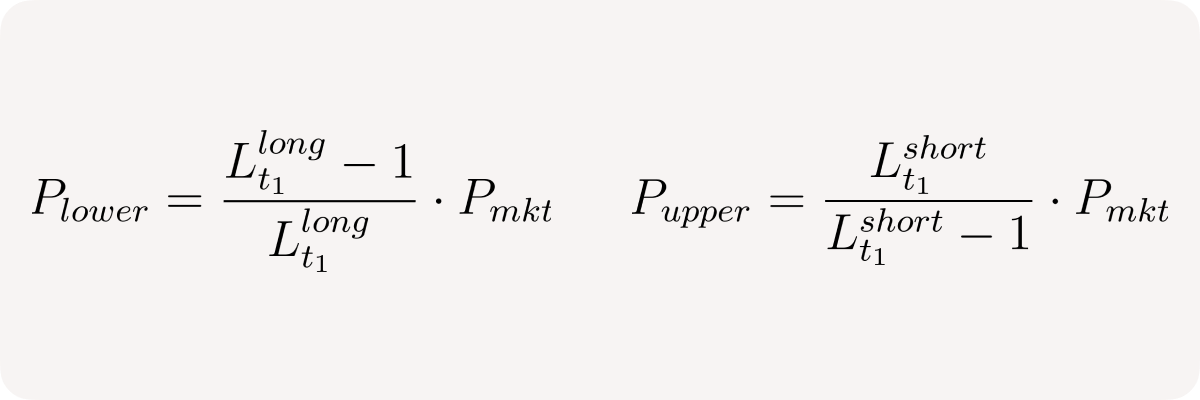
I’ve compiled a little spreadsheet for a curious reader to play around (copy the entire sheet to play with numbers) with the above formulas to grasp the concept better.
If we know marginal prices, we know exactly when either net long or net short position of our pool becomes zero - that’s where we could hedge it using Uni v3 concentrated liquidity: we must unwind the long position when market price reaches P_lower, and unwind the short position when market price reaches P_upper. I’ve covered this approach in the previous write-up on marginly risks in the Architecture considerations for Marginly v2 article.
Even though relative net long and net short position changes have neat mathematical expressions tied to leverage, considering both net long and net short positions separately and thus hedging them separately might be not that effective: why not hedge the total net position? But how do we do it? This is a subject of ongoing research in Marginly.





